Understanding and benchmarking JAX’s autodiff options

I’ve been fiddling around with JAX lately to learn about the foundation library for Pytorch’s main rivals such as Flax, Haiku or Elegy. It’s pretty obvious that Pytorch has the upperhand in the Deep Learning community, however Jax promises to deliver faster computation times (as usual, at the cost of being less flexible/pythonic/user friendly) and better adaptation to some accelerators like TPUs.

There is nothing better than trying out things for your self, so I embarked myself into a journey of understanding Jax and its main differences with Torch. In this blogpost, I’ll introduce and benchmark the some of the functions that make’s JAX essence.

Keep in mind that JAX is not a Deep Learning framework. As the creators say, JAX is Autograd and XLA, brought together for high-performance numerical computing. This is, numpy + autodiff on multiple accelerators (e.g. CPU, GPU, TPU), so it’s useful in multiple scientific fields, not just machine learning (although everything seems to be AI related nowadays :P)

Setting up our benchmark

Some imports to make our life easier plus a little decorator that will help us time functions

import matplotlib.pyplot as plt

from itertools import product
from functools import wraps
from random import choices, seed
from time import time
from numpy import median, nan

seed(123456)

def with_timing(return_t: bool = False, log: bool = True):
    """Decorator that times a function.
    
    It allows the user to retrieve or log the timing

    Args:
        return_t (bool, optional): If true, returns a (time, result) tuple
        log (bool, optional): If true, logs the time through loguru's logger
    """
    def decorator(f):
        @wraps(f)
        def wrap(*args, **kwargs):
            t0 = time()
            result = f(*args, **kwargs)
            tdiff = time() - t0
            if log:
                logger.info(f"{f.__name__} took {tdiff:.5f}s")
            return (result, tdiff) if return_t else result

        return wrap

    return decorator

JAX’s essence: grad and vmap

from jax import grad, jacfwd, jacrev, jit, random, vmap
from jax import numpy as jnp
from jaxlib.xla_extension import XlaRuntimeError

Here I’m importing the following functions:

• grad: computes the gradient (derivative) of any given function
• jacfwd, jacrev: compute the jacobian matrix of any given function
• jit: compiles any function to translate it to XLA
• vmap: applies (maps) any function over any axis of a JAX array

I’m not gonna cover pmap here, but it’s the same as vmap with device paralelization.

jit

jit (just in time) is one of JAX’s core functions. It’s a function decorator, resulting in it being compiled in order to make computations faster. It’s very convinient to use but it’s got it’s drawbacks, like just being able to use jax.numpy types, or not being able to use flow control python instructions (but you can use their equivalent in jax code)

@jit
def f(x,y):
    return jnp.array(x + y**2)

It’s not of much interest here as we’ll be always “jitting” our functions

grad

Alongside jit, grad it’s another. Given any scalar output function, it computes the gradient/derivative of this function. In order to see a practical example, let’s dust off calculus a bit. We have our function

\[f(x,y) = x + y^2\]

So, the gradient for that function would be:

\[\nabla f(x, y) = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right) = \left(1, 2y\right)\]

Now, without using autodiff, we’d have to explicitly write the formula for any given function we wanted. However, autodiff is here to help us! According to the expresion above, if we evaluate the gradient in $x=3, y=3$, the result would be

\[\nabla f(x, y)=(1,6)\]

x, y = 3., 3.
grad(f,0)(x,y), grad(f,1)(x,y)

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

(DeviceArray(1., dtype=float32, weak_type=True),
 DeviceArray(6., dtype=float32, weak_type=True))

And we can see that that is the case (0 (x) and 1 (y) indicate the argument number). Now, if we wanted to apply the same to a new function

\[g(x,y) = (x - y, f(x,y))\]

@jit
def g(x,y):
    return jnp.array([x-y, f(x,y)])

try:
    grad(g)(x,y)
except Exception as e:
    print(type(e))
    print(e)

<class 'TypeError'>
Gradient only defined for scalar-output functions. Output had shape: (2,).

We get an error since the gradient is only defined for scalar-output functions (in plain english, functions that return a single value). For these cases, we have the jacobian matrix as a generalization of the gradient

\[J_g(x, y) = \begin{bmatrix} \frac{\partial g_1}{\partial x} & \frac{\partial g_1}{\partial y} \\ \frac{\partial g_2}{\partial x} & \frac{\partial g_2}{\partial y} \end{bmatrix}\]

where

\[(g_1(x, y) = x - y)\]

and

\((g_2(x, y) = f(x, y))\).

Substituting the expressions, we get:

\[J_g(x, y) = \begin{bmatrix} \frac{\partial}{\partial x}(x - y) & \frac{\partial}{\partial y}(x - y) \\ \frac{\partial}{\partial x}(x + y^2) & \frac{\partial}{\partial y}(x + y^2) \end{bmatrix}\]

Simplifying the expressions further:

\[J_g(x, y) = \begin{bmatrix} 1 & -1 \\ 1 & 2y \end{bmatrix}\]

And again for our point

\[x=3, y=3\]

jnp.stack(
    [jacfwd(g,0)(x,y),jacfwd(g,1)(x,y)],
    -1
)

DeviceArray([[ 1., -1.],
             [ 1.,  6.]], dtype=float32)

That is the case

A lot of datapoints

What if instead of having a single point, we have two collections of points. Instead of running a for loop, jax provides the vmap functionality to map a function over an input. As you can see, jax is heavily functional programming oriented, and I like that a lot

xy = jnp.array([[1,1],[2,2],[3,3]]).astype('float')
def f_vec(xy):
    x,y = xy
    return f(x,y)
    
vmap(grad(f_vec), 0)(xy)

/tmp/ipykernel_22989/3535598499.py:1: UserWarning: Explicitly requested dtype float requested in astype is not available, and will be truncated to dtype float32. To enable more dtypes, set the jax_enable_x64 configuration option or the JAX_ENABLE_X64 shell environment variable. See https://github.com/google/jax#current-gotchas for more.
  xy = jnp.array([[1,1],[2,2],[3,3]]).astype('float')

DeviceArray([[1., 2.],
             [1., 4.],
             [1., 6.]], dtype=float32)

Et voilá, there we have our mapped function without slow loops. By changing vmap to pmap the process gets paralelized

Optimizing a Linear Layer

I’ll go now to the basic Deep Learning problem: computing the gradient of a linear layer. As usual, we have our problem setup

\[X_{(n \times p)} : \text{our data of n observations with p variables}\] \[W_{p \times o} : \text{The weights matrix with hidden dimension o}\]

So for any given record $X_i$ the forward pass would be \(forward(X_i, W_k) = W_1k * X_{i1} + \ldots + W_pk * X_{ip}\)

Where $W_k = [W_1, W_2,]

@jit
def forward(W, X):
    return X @ W

And the gradient would be

\[\frac{\partial forward}{\partial w_{jk}} = X_{ij}\]

The jacobian matrix will have dimensions: \((o,p)\), although it’s sparse since only $p$ weights contribute to each output $o$. The autodiff for the jacobian will however compute it for all the weights, so if we compute the gradients only for those non null combinations (‘vmap + grad’) it should be faster. I’m gonna benchmark 4 options to compute the gradients with respect to $W$

• test_jacfwd, test_jacrev: computing the full hessian of all the outputs. This should be less efficient because it will compute the gradient of each output $o_k$ with respect to all the weights and all observations, even though only one column $W{.k}$ contributes to each output. The code is shorter since we are not using vmap, jacfwd uses it internally.
• test_vmap_grad : should be the fastest, since we are computing the least ammount of gradients
• test_vmap_jacfwd, test_vmap_jacrev: it’s a combination of the two above, but it should still be slower.

The difference between jacfwd and jacrev is the way they are implemented: the former is better for tall matrices while the latter is better for wide matrices

@with_timing(return_t=True, log=False)
def test_jacfwd(W, X):
    return jacfwd(forward)(W, X).sum(axis=1)

@with_timing(return_t=True, log=False)
def test_vmap_grad(W, X):
    return vmap(
        lambda xi: vmap(lambda wi: grad(forward)(wi, xi), in_axes=-1, out_axes=-1)(W)
    )(X)


@with_timing(return_t=True, log=False)
def test_vmap_jacfwd(W, X):
    return vmap(lambda xi: jacfwd(forward)(W, xi))(X).sum(axis=1)


@with_timing(return_t=True, log=False)
def test_jacrev(W, X):
    return jacrev(forward)(W, X).sum(axis=1)


@with_timing(return_t=True, log=False)
def test_vmap_jacrev(W, X):
    return vmap(lambda xi: jacrev(forward)(W, xi))(X).sum(axis=1)


tests = [test_jacfwd, test_vmap_grad, test_vmap_jacfwd, test_jacrev, test_vmap_jacrev]
tests = {t.__name__: t for t in tests}

This is our test loop, in which we will iterate over different combinations of $n,p$ and $o$, creating random matrices each time. We’ll take the median time over $nreps$ and then plot the results

def test_loop(
    ns: list[int],
    ps: list[int],
    os: list[int],
    nreps: int = 200,
    tests: dict[str] = tests,
):
    setups = list(product(ns, ps, os))
    avg_times = {setup: {} for setup in setups}
    for n, p, o in setups:
        xkey, wkey = random.PRNGKey(0), random.PRNGKey(1)
        X = random.uniform(xkey, (n, p))
        W = random.uniform(wkey, (p, o))

        for tname, test in tests.items():
            test_times = []
            for _ in range(nreps):
                try:
                    _, t = test(W, X)
                except XlaRuntimeError:
                    t = nan
                test_times.append(t)
            avg_times[(n, p, o)][tname] = median(test_times)

    return avg_times


test_pallete = {test: "#" + "".join(choices("0123456789ABCDEF", k=6)) for test in tests}


def plot_avg_times(avg_times, tests: dict = tests):
    ns = sorted({n for n, _, _ in avg_times})
    ps = sorted({p for _, p, _ in avg_times})
    os = sorted({o for _, _, o in avg_times})

    n_plots = len(os) * len(ns)
    fig, axs = plt.subplots(n_plots, 1, figsize=(10, 10))
    if n_plots == 1:
        axs = [axs]
    else:
        axs.flatten()

    for o_n, ax in zip(product(os, ns), axs):
        o, n = o_n
        for test in sorted(tests):
            times = [avg_times[(n, p, o)][test] for p in ps]
            ax.plot(times, label=test, color=test_pallete[test])
            ax.set_xticks(range(len(ps)), ps)
            ax.set_title(f"o = {o}, n = {n}")
            ax.set_xlabel("p")
            ax.set_yscale("log")
            # ax.legend()
    lines, labels = ax.get_legend_handles_labels()
    labels = [label.replace("test_", "") for label in labels]
    fig.legend(lines, labels, loc="lower center", ncol=4)

We’ll be using a tall wide matrix ($p<o$), so jacrev should be faster than jacfwd

tall_times = test_loop(ns=[5, 10], ps=[8, 16, 64, 256, 512], os=[2, 5])
plot_avg_times(tall_times)

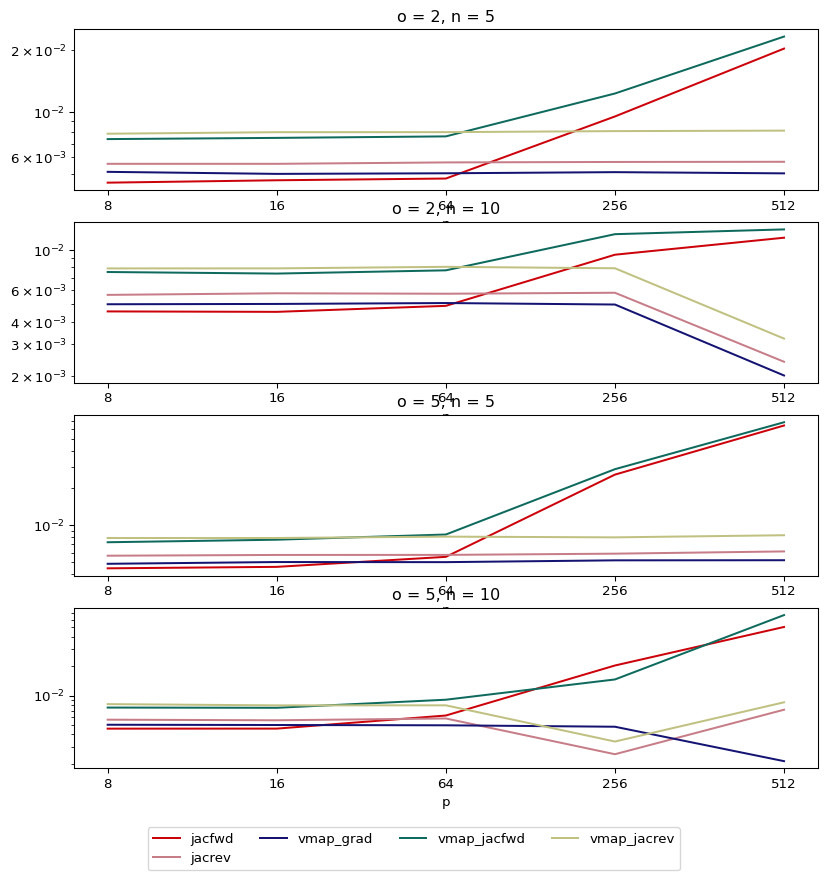
As expected, the fastest, even when using two functions is vmap + grad, and also jacfwd is slower than jacrev since $p>o$, and as $p$ grows, this difference is increased

Conclusion

In this blogpost we looked at the fundamental JAX functions and how to get an edge on computing times even when it might seem less efficient. Stay tuned for new posts regarding JAX and its ecosystem!